Wonderlijke Wiskunde (1)

Aankondiging workshop op de studiedag over DIVERSITEIT van de Nederlandse Vereniging van Wiskundeleraren
zaterdag 6 november 2021

L1 Wonderlijke Wiskunde
Dirk Adrichem

Deze workshop is bedoeld voor docenten in het voortgezet onderwijs. De lessen zijn aanvankelijk ontwikkeld om basisscholieren, die extra uitdaging nodig hadden, een dieper inzicht in de ruimte aan te reiken, zonder middelbare-school-boeken te gebruiken. De instap is uniek, eenvoudig en visueel.

Dualiteit is de axiomatische symmetrie tussen lijnen en punten, die terug te vinden is in de postulaten van Euclides. De elementen van Euclides zijn punt, lijn en vlak. De ruimte wordt gewoonlijk opgevat als puntenverzameling, maar ruimte is evengoed een lijnenverzameling en een vlakkenverzameling.

Lijn en punt worden als gelijkwaardige vlak-meetkundige elementen geïntroduceerd. Het dominante begrip punt wordt tegenover het begrip copunt geplaatst. De copuntenverzameling heet coruimte. In de vlakke meetkunde is de coruimte een lijnenruimte. Aan een toepassing in een Zebraboekje wordt gewerkt. Nu al interesse? Kom naar deze werkgroep!

samenvatting van de workshop
wonderlijke wiskunde over
dualiteit in de euclidische meetkunde

November 2021

Op de workshop wonderlijke wiskunde van de studiedag van de NVvW was door een divers gezelschap van 15 deelnemers ingetekend. Naast verwachte wiskundeleraren waren twee kleuteronderwijzers, twee wiskundestudenten en een hoogleraar meetkunde aanwezig. Deze onverwachte diversiteit vroeg om een improvisatie, die met een spontaan applaus afsloot.

Het thema van de studiedag, diversiteit, werd in deze workshop belicht vanuit het standpunt dat punt, lijn en vlak ruimtelijke elementen zijn. De deelnemers konden beleven hoe een onbekende kant van de vlakke meetkunde onverwacht tevoorschijn komt, wanneer de lijn als element in een gelijkwaardige positie tegenover het anders zo dominante puntbegrip komt te staan.

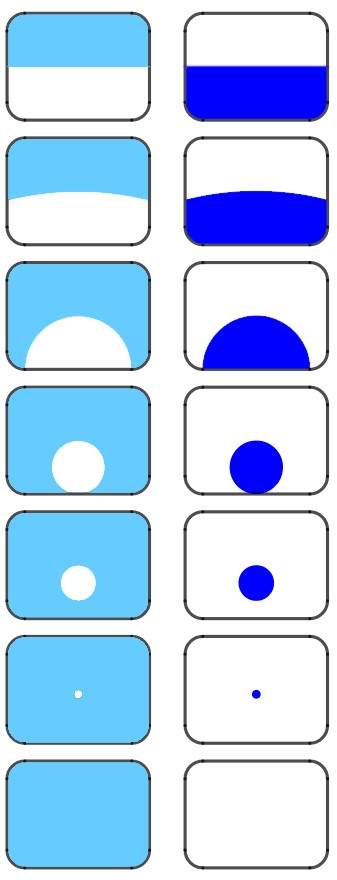
Drie oefeningen werden behandeld, die elk op zich in de klas een of meer lesuren zouden kunnen beslaan. Euclides gebruikte, naast het begrip punt, de begrippen lijnstuk en vlakdeel, die verwijzen naar de huidige begrippen lijn en vlak. Lijn en vlak zijn, naast het begrip punt, elementaire meetkundige bouwstenen. Bij opdeling van een element in stukken en delen, verdwijnt de essentie, zoals bij vee in een slachterij. De resterende delen van het geheel krijgen eigen namen. De ruimtelijke elementen punt, lijn en vlak zijn ondeelbare gehelen. In de vlakke meetkunde wordt gewerkt met de elementen punt en lijn. De eerste oefening introduceerde punt en lijn als grensvormen van de cirkel. In plaats van de cirkel voldoet hiervoor elke gesloten curve.

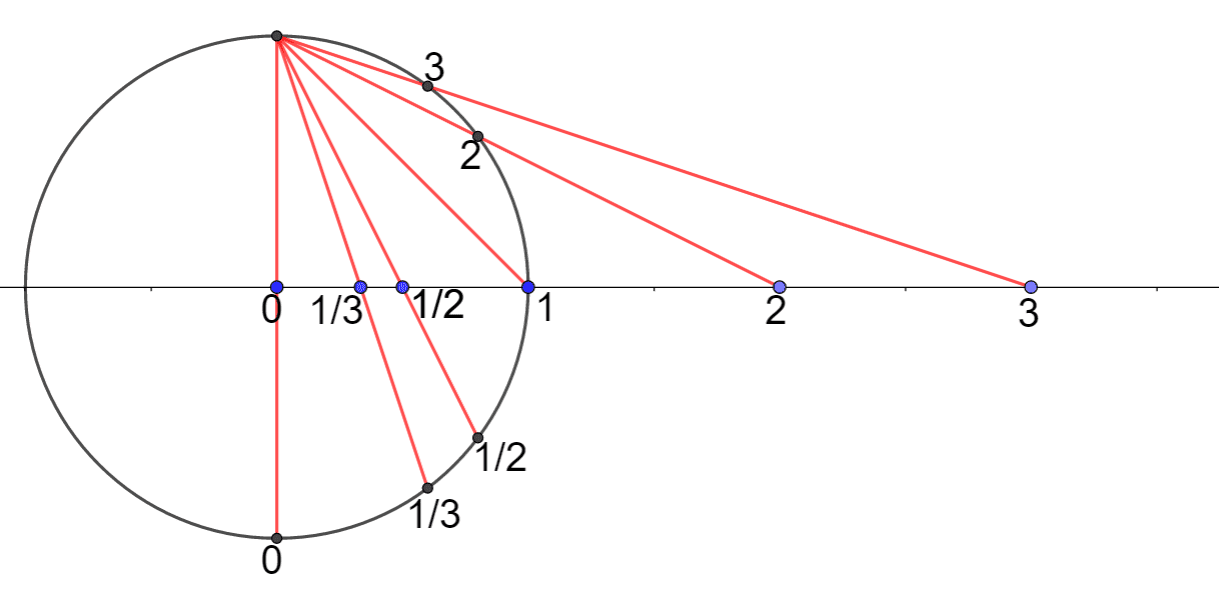
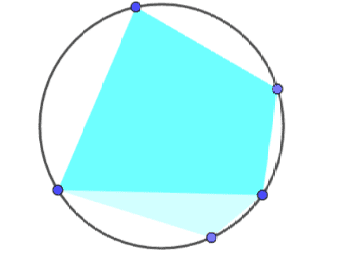
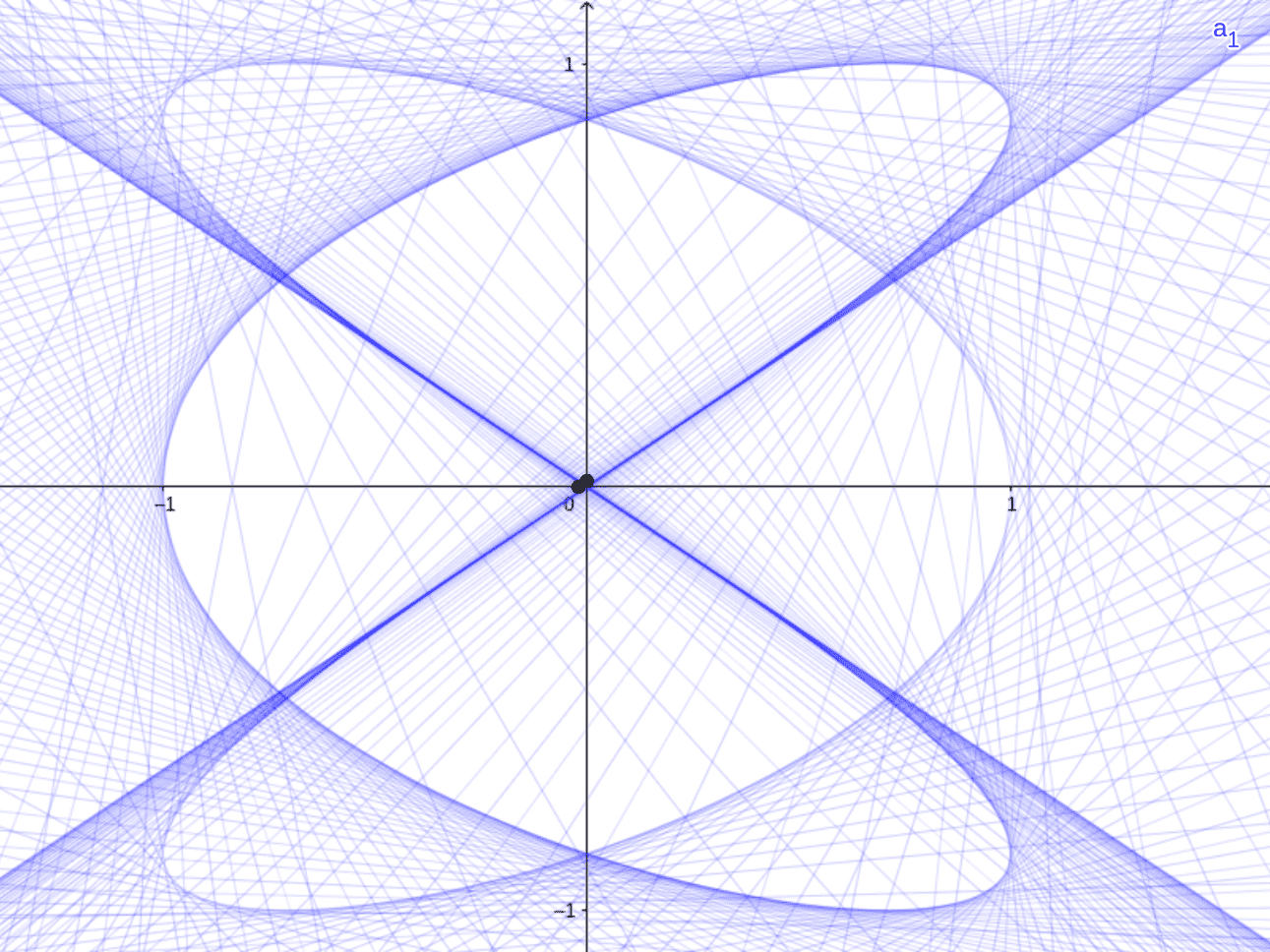
De elementen punt en lijn brengen allereerst twee grondvormen (Grundgebilde) voort: de lijnenwaaier (Geradenbüschel, pencil of lines, faisceau) en de puntenrij (Punktreihe, range of points, points colinéaire). N.B. de veelgebruikte lijn als functie is puntenrij. De tweede oefening liet cirkels ontstaan uit twee congruente lijnenwaaiers. Dit hangt samen met de uit de schoolwiskunde bekende stelling van de constante (omtreks-)hoek bij de cirkel. De derde oefening liet parabolen ontstaan uit twee congruente puntenrijen. Dit hangt samen met de in de schoolwiskunde onbekende stelling van de constante (brandpunts-)hoek bij de parabool. Het verband tussen beide constante hoekstellingen heet dualiteit. Waar komt dit duale verband vandaan? Voor het antwoord op deze vraag gingen we terug naar de vijf meetkundige postulaten (grondstellingen) van Euclides. Eigenschappen van deze grondstellingen doorkleuren het gehele bouwwerk van euclidische stellingen.

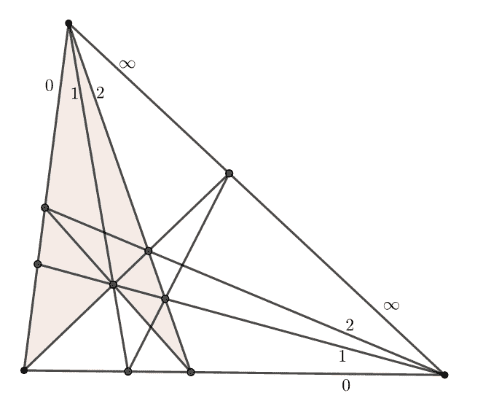
Om zicht te krijgen op dualiteit, werden metrische begrippen opzij gezet. Daarom konden het derde en vierde postulaat het veld ruimen en werden de eerste twee postulaten tot het eerste incidentiepostulaat teruggebracht:

"Twee punten zijn incident met één enkele lijn".

Incident betekent "liggen op", "gaan door" en dergelijke. Het laatste postulaat zegt: "Twee lijnen hebben één enkel punt òf één richting gemeenschappelijk". Met axiomatische permissie van het eerste postulaat treedt het begrip richting op als punt: "Een punt en een richting hebben één enkele lijn gemeenschappelijk". Het tweede incidentiepostulaat luidt dan:

"Twee lijnen zijn incident met één enkel punt"

met de aantekening dat een richting axiomatische toestemming heeft in te vallen als punt.

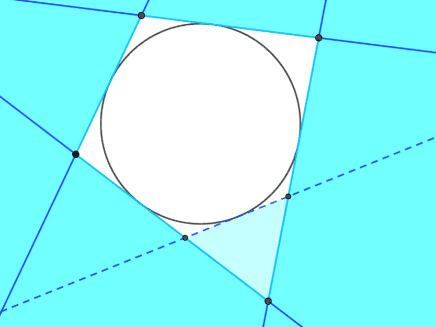
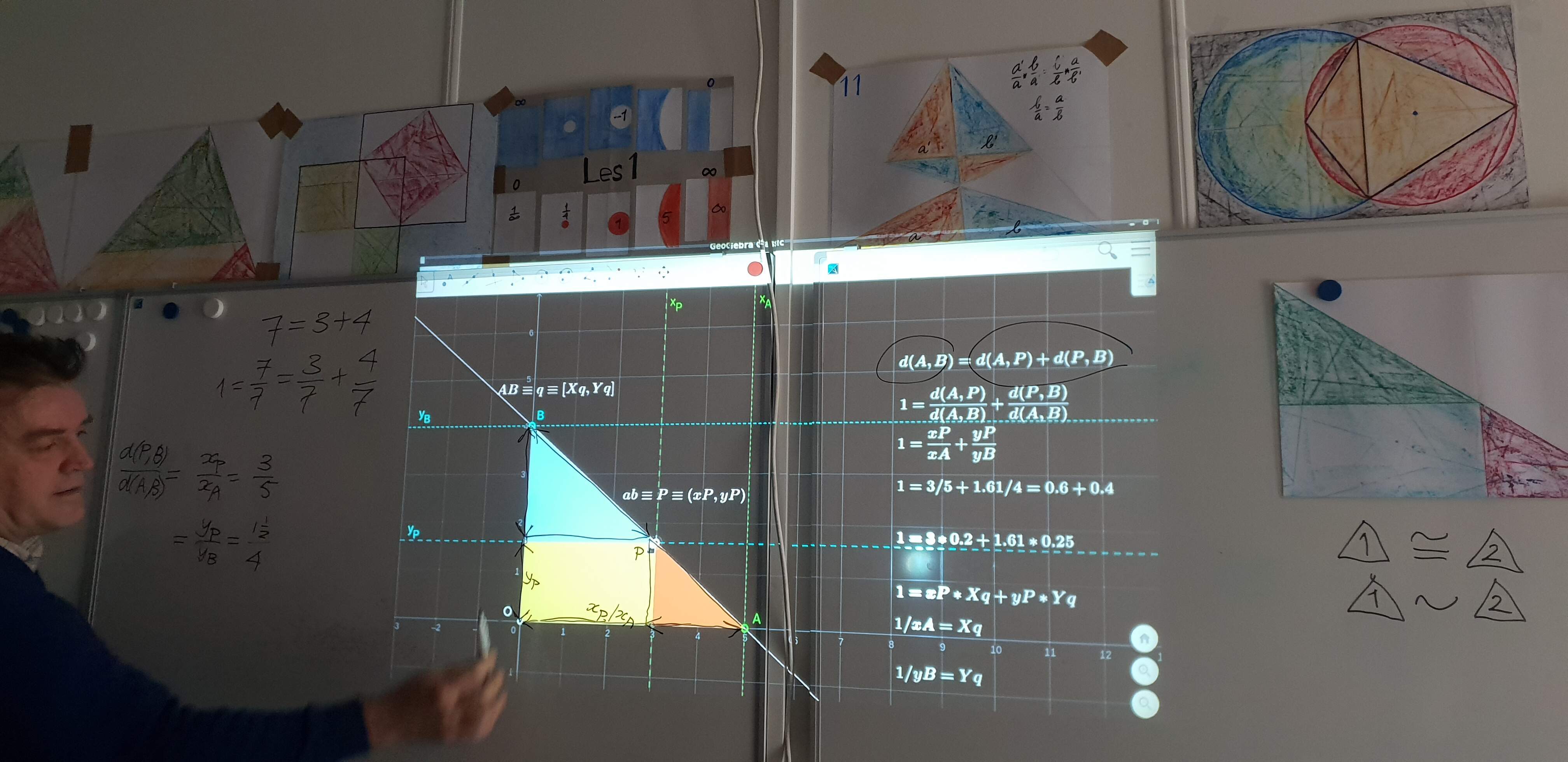
Tenslotte kwam het nauw verwante begrip polariteit aan bod. Polariteit is paarvorming tussen ruimte en coruimte. De verzamelingenleer noemt dit een 1-1-relatie en ook wel bijectie. In de schoolwiskunde van afgelopen 100 jaar is meermaals gepoogd de pooltheorie te introduceren. Het is tot nu toe niet gelukt deze prachtige theorie op verantwoord wijze in te voeren als eigenschap van de diverse kegelsneden. Met behulp van met differentiëren gevonden vuistregels als "eerlijk delen" en "halve substitutie" werden vraagstukken over polariteit gemaakt, zonder dat duidelijk werd waarom de poolrelatie een bijectie is en waarom het raaklijnverschijnsel optreedt. Mogelijk dat de centrale begrippen coruimte en de zelfduale incidentierelatie (axX + byY + c(xY + yX) + d(x + X) + e(y + Y) = 1 of 0, zie de homepage) een uitkomst bieden. De kegelsneden kunnen in dat geval worden opgevat als de polariteit (x, y) ≡ (X, Y) of [X, Y] ≡ [x, y] in combinatie met een zelfduale incidentierelatie:

axx + byy +2cxy + 2dx +2ey = 1 of 0

oneigenlijke punten

Oneigenlijke punten kunnen niet worden toegevoegd aan de euclidische ruimte. Ze zijn al aanwezig in de vorm van richtingen. De projectieve ruimte is dus geen mysterieuze uitbreiding van de euclidische, maar slechts een erkenning dat richtingen als punten kunnen worden opgevat.

points at infinity

Points at infinity cannot be added to euclidian space. They are already present in the form of directions. So the projective space is not a mysterious extension of the euclidian one, but only an acknowledgement that directions can be seen as points.

DUALITEIT

De lijn is de grensvorm van een groeiende cirkel. Het punt is de grensvorm van een krimpende cirkel. Lijn en punt zijn daarom tegengestelde elementen van de vlakke meetkunde. Dualiteit is de kwalitatieve gelijkwaardigheid tussen deze tegengestelde elementen.

Van onder naar boven groeit rechts in de afbeelding hiernaast een ruimtegebied. Links groeit van boven naar onder een coruimtegebied.

Deze bewegingen vormen samen een rondgaand proces van een groeiende diameter met de positieve getallen rechts en de negatieve links. De coruimte heet dan ook wel "negatieve ruimte".

In de afbeelding hieronder is dit rondgaande proces uitgebeeld in een getallencirkel. Linksom stijgen de getallen continu, zelfs bij het passeren van oneindig. Evenals nul is oneindig immers gelijk aan zijn negatieve waarde: ∞ = 1/0 = 1/(-0) = -1/0 = - ∞.

duality

The line is the limit of a growing circle. The point is the limit of a contracting circle. Line and the point are thus opposite elements in plane geometry. Duality is the qualitative equivalence between these opposite elements.

In the image above at the right from bottom to top a spacial area is growing. From top to bottom a co-spacial area is growing at the left.

These movements together form a circular process of a growing diameter with positive numbers at the right and negative at the left. Co-space is also called "negative space".

In the image to the left, this circular process is depicted in a number circle. Counterclockwise the numbers increase continuously even when passing infinity. Just like zero, infinite is equal to it's negative value: ∞ = 1/0 = 1/(-0) = -1/0 = - ∞.

CORUIMTE

Coruimte is de verzameling van copunten. Een ander woord voor "copunt" is "hypervlak". Het coruimte-concept blijkt zeer productief. Een gevolg is gelijkwaardigheid tussen punt en lijn in de vlakke meetkunde.

Zowel het kwantitatieve aspect, als de kwalitatieve kant van de ruimte wordt belicht.

Berekeningen met raaklijnen zijn overzichtelijk met de wiskunde die hier wordt geïntroduceerd.

Co-space

Co-space is the set of co-points. "Co-point" means as much as "hyperplane". The concept of co-space turns out to be very productive. A result is equivalence between point and line in plane geometry.

Both the quantitative aspect and the qualitative side of space are highlighted.

Tangent calculations are straightforward with the math introduced here.

complementaire dimensie

Een copunt is een element in de coruimte. Het voorvoegsel "co" is een samentrekking van "complementair". Dit woordgebruik verwijst naar het feit dat de verhoogde dimensies van copunt en punt elkaars complement zijn:

dim#(punt) + dim#(copunt) = dim#(ruimte)

Bovendien: dim#(∅) = 1 + dim(∅) = 1 + (-1) = 0. Deze mooie uitkomst voor de lege verzameling is een extra aanbeveling voor het verhoogde dimensiegetal.

complementary dimension

A co-point is an element in co-space. The prefix "co" is a contraction of "complementary". This word usage refers to the fact that the raised dimensions of co-point and point are each other's complement:

dim#(point) + dim#(co-point) = dim#(space)

Besides: dim#(∅) = 1 + dim(∅) = 1 + (-1) = 0
This nice result for the empty set is an additional recommendation for the increased dimension number.

Polariteit

Polariteit is de quantitatieve gelijkwaardigheid van duale elementen. Een eerste vereiste voor polariteit is dat ruimte en coruimte isomorf zijn. Hun elementen staan dus in een 1-op-1 relatie met elkaar.
Een tweede vereiste is een zelfduale incidentierelatie:

axX + byY + c(xY + Xy) + d(x + X) + e(y + Y) = 1 of 0

Een derde vereiste zijn gelijke positiegetallen voor poolpartners.

Een ruimtemodel is een speciaal geval van de incidentierelatie, zoals: xX + yY = 1, die in dit geval de eenheidscirkel voortbrengt. Elke specifieke kegelsnede komt voort uit een specifiek zelfduaal ruimtemodel.
Polariteit is hiermee onafhankelijk van kegelsneden afgeleid uit het co-ruimte-concept.

Polariteit in combinatie met incidentie dekt het raaklijnbegrip bij kegelsneden.

Polarity

Polarity is the quantitative equivalence of dual elements. The first condition for polarity is that space and co-space are isomorphic. The second condition is a self-dual incidence relationship:

axX + byY + c(xY + Xy) + d(x + X) + e(y + Y) = 1 or 0

The third condition are equal position numbers for pole partners.

A space model is a special case of the incidence relation, such as: xX + yY = 1, wich in this case produces the unit circle. Every conic arises from a specific self-dual space model. Polarity is therefore derived from the co-space concept independently of conics.

Polarity combined with incidence covers the tangent concept in conic sections.

"eerlijk delen"

Deze website dankt haar bestaan aan de beschrijving van wiskundige dualiteit door Joseph Gergonne (1826) en Jean-Victor Poncelet (1822).

Merkwaardig is dat polariteit wel, maar dualiteit niet aan bod komt in de analytische schoolmeetkunde. Schoolwiskunde leert ten opzichte van een kegelsnede de vergelijking te vinden van de poollijn van een punt (x, y). Deze methode is bekend als "eerlijk delen" en ook wel als "halve substitutie". Om raaklijnen aan een kegelsnede te vinden wordt dezelfde methode gebruikt.
Kwalitatieve gelijkwaardigheid van punt en lijn komt niet aan bod, omdat de lijn niet als zelfstandig element geldt, maar wordt opgevat als puntenverzameling. Men negeert daarbij dat de lijn net zo min een puntenreeks is als dat het punt een lijnenwaaier is.
Gevolg is dat ook de kwantitatieve gelijkwaardigheid van de polariteit niet onderwezen wordt. Polariteit wordt beschouwd als een bijzondere eigenschap van kegelsneden. Deze website laat zien dat kegelsneden een gevolg zijn van de gelijkwaardigheid van ruimte en coruimte.
Het zal niet de bedoeling zijn geweest, maar de uitdrukkingen "halve substitutie" en "eerlijk delen", gewoonlijk gezien en gebruikt als onschuldig ezelsbruggetje, verwoorden plotseling het principe van gelijkwaardigheid binnen het coruimte-concept.

"fair sharing"

This website owes its existence to the description of mathematical duality by Joseph Gergonne (1826) and Jean-Victor Poncelet (1822).
It is remarkable that polarity does, but duality does not appear in analytic school geometry.
School mathematics teaches to find the equation of the polar line of a point (x, y) with respect to a conic section. This method is known in dutch as ¨fair sharing¨ or ¨half substitution¨. The same method is used for finding tangents to a conic.
Qualitative equivalence of point and line is not considered, because the line does not count as an element on its own. One ignores that the line is no more a range of points than the point is a pencil of lines.
As a result, the quantitative equivalence of polarity is not taught either. Polarity is considered a special property of conics. This website shows that conics are a result of the equivalence of space and co-space.

It may not have been the intention, but the expressions "half substitution" and "fair sharing", commonly seen and used as an innocent mnemonic, suddenly articulate the principal of equivalence within the co-space concept.

Hans freudenthal in Mathematik als pädagogische aufgabe (1973), (pag 85):

"Symmetrie-Argumente spielen auch in der Mathematik eine Rolle, wenn die traditionelle Mathematik (oder vielmehr die traditionelle Schulmathematik) sie auch kaum anerkennt und sie am liebsten verdunkelt, unterschlägt, durch unsachliche Algorithmen ersetzt - siehe die Verdrängung von Symmetrie-Argumenten in der Geometrie durch die algorithmische Anwendung von Kongruenzsätzen, in der Algebra durch algorithmische Rechnungen."

ionawiskunde